 数据结构与算法--跳表
数据结构与算法--跳表
# 数据结构与算法--跳表
# 一、简介
跳表全称叫做跳跃表,本质上就是有序链表 + 多级索引 + 随机技术,它在有序链表上面增加了多级索引,另外采用随机技术来维护数据结构的平衡性。相对于有序链表时间复杂度O(n)而言,跳表的查询、插入、删除的平均时间复杂度都为 O(logn)
采用这种随机技术,跳表中的搜索、插入、删除操作的时间均为O(logn),然而,最坏情况下时间复杂性却变成O(n)。相比之下,在一个有序数组或链表中进行插入/删除操作的时间为O(n),最坏情况下为O(n)。
Leetcode--1206. 设计跳表 (opens new window)
# 二、跳表的实现原理图
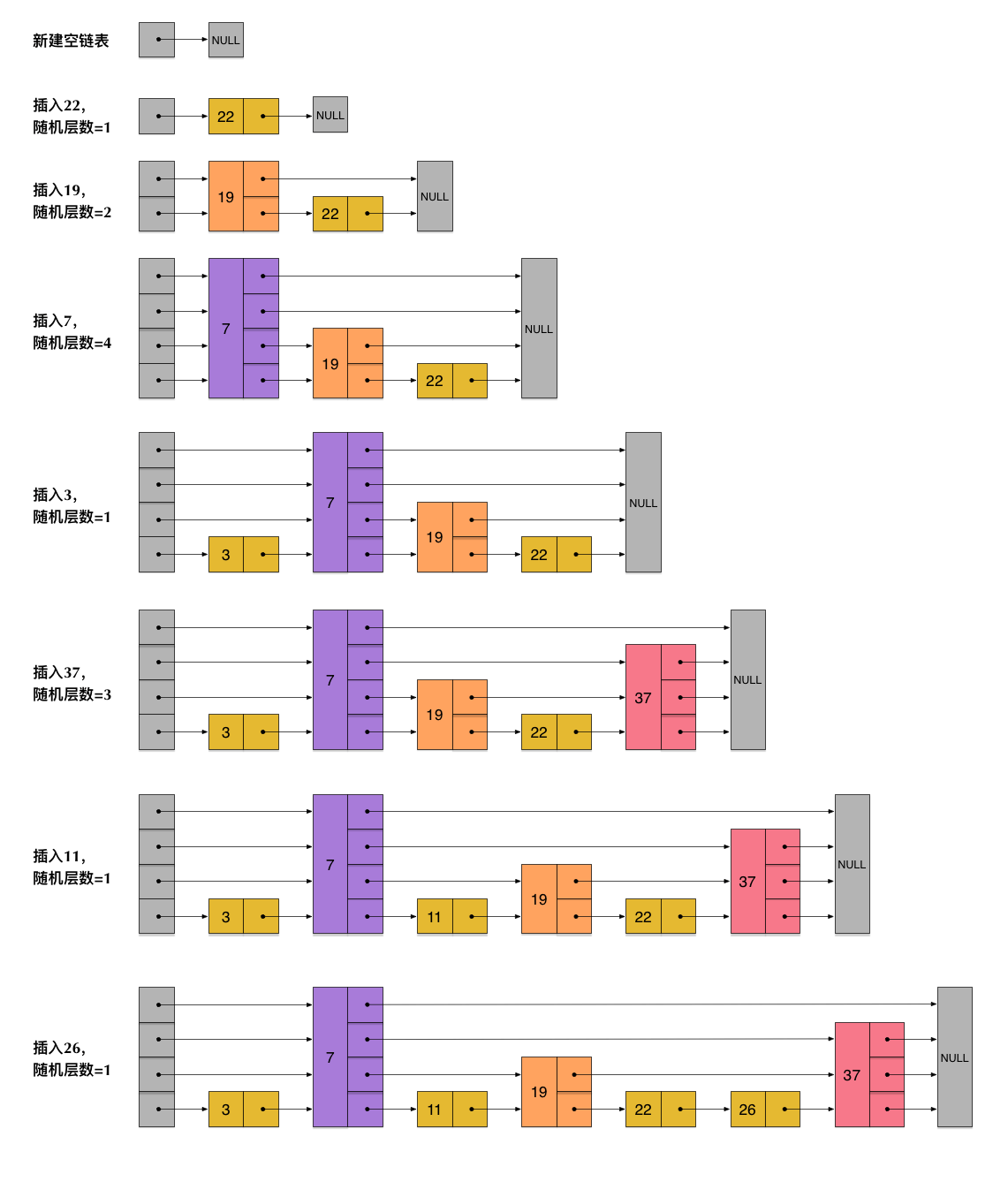
# 三、跳表的代码实现
# 3.1、跳表的数据结构
class SkipListNode {
Integer val; //节点值
SkipListNode[] next;// 节点在不同层的下一个节点
public SkipListNode(Integer val, int level) { // level表示当前节点在跳表中索引几层
this.val = val;
this.next = new SkipListNode[level];
}
}
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
# 3.2、跳表的查询
/**
* Step1: 从跳表的最大层数 skipLevel 开始查找最接近 target 的节点
* Step1.1: 如果查找到的节点的下一个节点等于 target,返回true
* Step1.2: 否则,继续向下查找
*
* @param target
* @return
*/
public boolean search(int target) {
SkipListNode searchNode = head;
for (int i = skipLevel - 1; i >= 0; i--) {
//Step1: 从跳表的最大层数 skipLevel 开始查找最接近 target 的节点
searchNode = findClosestNode(searchNode, i, target);
//Step1.1: 如果查找到的节点的下一个节点等于 target,返回true
if (searchNode.next[i] != null && searchNode.next[i].val == target) {
return true;
}
//Step1.2: 否则,继续向下查找
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 3.3、跳表的删除
/**
* Step1: 从跳表的最大层数 skipLevel 开始查找最接近 target 的节点
* Step2: 如果查找到的节点的下一个节点等于 target,那么删除下一个节点,并且更新 skipLevel
* Step3: 重复 Step2
*
* @param target
* @return
*/
public boolean erase(int target) {
boolean res = false;
SkipListNode searchNode = head;
for (int i = skipLevel - 1; i >= 0; i--) {
//Step1: 从跳表的最大层数 skipLevel 开始查找最接近 target 的节点
searchNode = findClosestNode(searchNode, i, target);
if (searchNode.next[i] != null && searchNode.next[i].val == target) {
//Step2: 如果查找到的节点的下一个节点等于 target,那么删除下一个节点,并且更新 skipLevel
searchNode.next[i] = searchNode.next[i].next[i];//删除节点
if(head.next[i] == null) skipLevel--;//对skipLevel 进行更新
res = true;
continue;
}
}
return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 3.4、跳表的插入
/**
* Step1: 获取随机层数并创建节点
* Step2: 从Step1的随机层往下一层层添加节点
* Step3: 如果head.next[i]节点为空,那么直接head.next[i]直接指向新节点
* Step4: 如果head.next[i]节点不为空,开始查找当前层最接近 target 的节点
* Step5: 在Step4中找到的节点后插入新节点
*
* @param target
*/
public void add(int target) {
//Step1: 获取随机层数并创建节点
int level = randomLevel();
SkipListNode newNode = new SkipListNode(target, level);
SkipListNode searchNode = head;
//Step2: 从Step1的随机层往下一层层添加节点
for (int i = level - 1; i >= 0; i--) {
if (searchNode.next[i] == null) {//Step3: 如果head.next[i]节点为空,那么直接head.next[i]直接指向新节点
searchNode.next[i] = newNode;
} else {
//Step4: 如果head.next[i]节点不为空,开始查找当前层最接近 target 的节点
searchNode = findClosestNode(searchNode, i, target);
//Step5: 在Step4中找到的节点后插入新节点
SkipListNode tmp = searchNode.next[i];
searchNode.next[i] = newNode;
newNode.next[i] = tmp;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 3.5、完整代码
class Skiplist {
private static final int MAX_LEVEL = 32;//跳表最大层数
private static final double P_FACTOR = 0.25;//跳表随机因子
private int skipLevel;//当前跳表层数
private SkipListNode head;
public Skiplist() {
this.head = new SkipListNode(null, MAX_LEVEL);
this.skipLevel = 0;
}
/**
* Step1: 从跳表的最大层数 skipLevel 开始查找最接近 target 的节点
* Step1.1: 如果查找到的节点的下一个节点等于 target,返回true
* Step1.2: 否则,继续向下查找
*
* @param target
* @return
*/
public boolean search(int target) {
SkipListNode searchNode = head;
for (int i = skipLevel - 1; i >= 0; i--) {
//Step1: 从跳表的最大层数 skipLevel 开始查找最接近 target 的节点
searchNode = findClosestNode(searchNode, i, target);
//Step1.1: 如果查找到的节点的下一个节点等于 target,返回true
if (searchNode.next[i] != null && searchNode.next[i].val == target) {
return true;
}
//Step1.2: 否则,继续向下查找
}
return false;
}
/**
* Step1: 获取随机层数并创建节点
* Step2: 从Step1的随机层往下一层层添加节点
* Step3: 如果head.next[i]节点为空,那么直接head.next[i]直接指向新节点
* Step4: 如果head.next[i]节点不为空,开始查找当前层最接近 target 的节点
* Step5: 在Step4中找到的节点后插入新节点
*
* @param target
*/
public void add(int target) {
//Step1: 获取随机层数并创建节点
int level = randomLevel();
SkipListNode newNode = new SkipListNode(target, level);
SkipListNode searchNode = head;
//Step2: 从Step1的随机层往下一层层添加节点
for (int i = level - 1; i >= 0; i--) {
if (searchNode.next[i] == null) {//Step3: 如果head.next[i]节点为空,那么直接head.next[i]直接指向新节点
searchNode.next[i] = newNode;
} else {
//Step4: 如果head.next[i]节点不为空,开始查找当前层最接近 target 的节点
searchNode = findClosestNode(searchNode, i, target);
//Step5: 在Step4中找到的节点后插入新节点
SkipListNode tmp = searchNode.next[i];
searchNode.next[i] = newNode;
newNode.next[i] = tmp;
}
}
}
/**
* Step1: 从跳表的最大层数 skipLevel 开始查找最接近 target 的节点
* Step2: 如果查找到的节点的下一个节点等于 target,那么删除下一个节点,并且更新 skipLevel
* Step3: 重复 Step2
*
* @param target
* @return
*/
public boolean erase(int target) {
boolean res = false;
SkipListNode searchNode = head;
for (int i = skipLevel - 1; i >= 0; i--) {
//Step1: 从跳表的最大层数 skipLevel 开始查找最接近 target 的节点
searchNode = findClosestNode(searchNode, i, target);
if (searchNode.next[i] != null && searchNode.next[i].val == target) {
//Step2: 如果查找到的节点的下一个节点等于 target,那么删除下一个节点,并且更新 skipLevel
searchNode.next[i] = searchNode.next[i].next[i];//删除节点
if(head.next[i] == null) skipLevel--;//对skipLevel 进行更新
res = true;
continue;
}
}
return res;
}
//找到当前level层 node.val 最接近 target 的节点, node.val < target
//注意,此处有序链表从小到大排列
private SkipListNode findClosestNode(SkipListNode node, int level, int target) {
while (node.next[level] != null && node.next[level].val < target) {
node = node.next[level];
}
return node;
}
//随机一个层数,若层数大于等于 skipLevel ,则更新 skipLevel
private int randomLevel() {
int lvl = 1;
while (Math.random() < P_FACTOR && lvl < MAX_LEVEL) {
lvl++;
}
if(lvl >= skipLevel) skipLevel = lvl;
return lvl;
}
class SkipListNode {
Integer val; //节点值
SkipListNode[] next;// 节点在不同层的下一个节点
public SkipListNode(Integer val, int level) { // level表示当前节点在跳表中索引几层
this.val = val;
this.next = new SkipListNode[level];
}
}
// public void printAll_beautiful() {//打印跳表结构
// System.out.println("#############################################################################################################################");
// SkipListNode p = head;
// SkipListNode[] c = p.next;
// SkipListNode[] d = c;
// //int[] data = new int[all_count];
// int maxLevel = c.length;
// SkipListNode[] s = c;
// HashMap<Integer, Integer> map = new HashMap<>();
// for (int i = 0; s[0] != null; i++) {
// map.put(i, s[0].val);
// s = s[0].next;
// }
// //System.out.println(map);
// //System.out.println(Arrays.toString(data));
// for (int i = maxLevel - 1; i >=0; i--) {
// if(d[i] == null) continue;
// System.out.printf("%2d层:", i);
// int j = 0;
// do {
// int value;
// if (d[i] != null) {
// value = d[i].val;
// while (value != map.get(j++)) {
// System.out.print("-----");
// }
// System.out.printf("%2d---", value);
// }
// } while (d[i] != null && (d = d[i].next)[i] != null);
// System.out.println();
// d = c;
// }
// }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
参考资料:
