数据结构与算法--LRU算法

一、简介

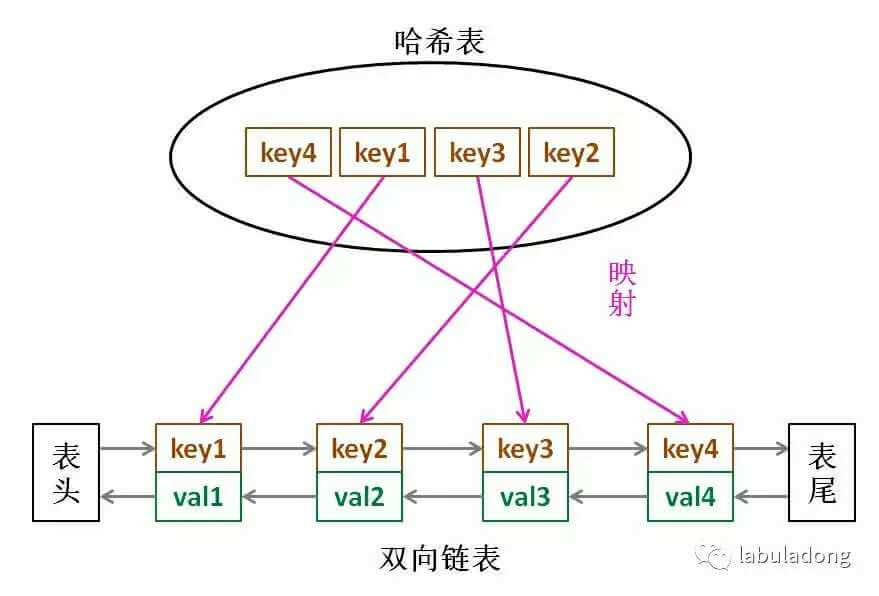
LRU 的全称是 Least Recently Used(最近最少使用)，是一种缓存淘汰策略，它是根据时间维度来选择将要淘汰的元素，即删除掉最长时间没被访问的元素据。它的底层是 哈希表 + 双链表 实现的，查找和添加的时间复杂度都是O(1)，Java中的LinkedHashMap就是这样的一种数据结构。

剑指 Offer II 031. 最近最少使用缓存 (opens new window)

二、LRU算法的代码实现

2.1、双链表的节点类

class DLinkedNode{//双链表节点类
        int key,val;
        DLinkedNode pre,next;
        public DLinkedNode(int _key,int _val){
            this.key = _key;
            this.val = _val;
        }
 }

2.2、双链表的实现类

class DLinkedList{//双链表
       DLinkedNode head,tail;//链表首尾结点

       public DLinkedList(){
           this.head = new DLinkedNode(-1,-1);
           this.tail = new DLinkedNode(-1,-1);
           head.next = tail;
           tail.pre = head;
       }

       public void addToHead(DLinkedNode node){//将节点添加到头部
           node.pre = head;
           node.next = head.next;
           head.next.pre = node;
           head.next = node;
       }

       public void moveToHead(DLinkedNode node){//将某个访问后的节点添加到头部
           removeNode(node);
           addToHead(node);
       }

       public void removeNode(DLinkedNode node){//删除某个节点
           node.pre.next = node.next;
           node.next.pre = node.pre;
       }

       public DLinkedNode removeTail(){//删除尾部结点
           DLinkedNode res = tail.pre;
           removeNode(res);
           return res;
       }

   }

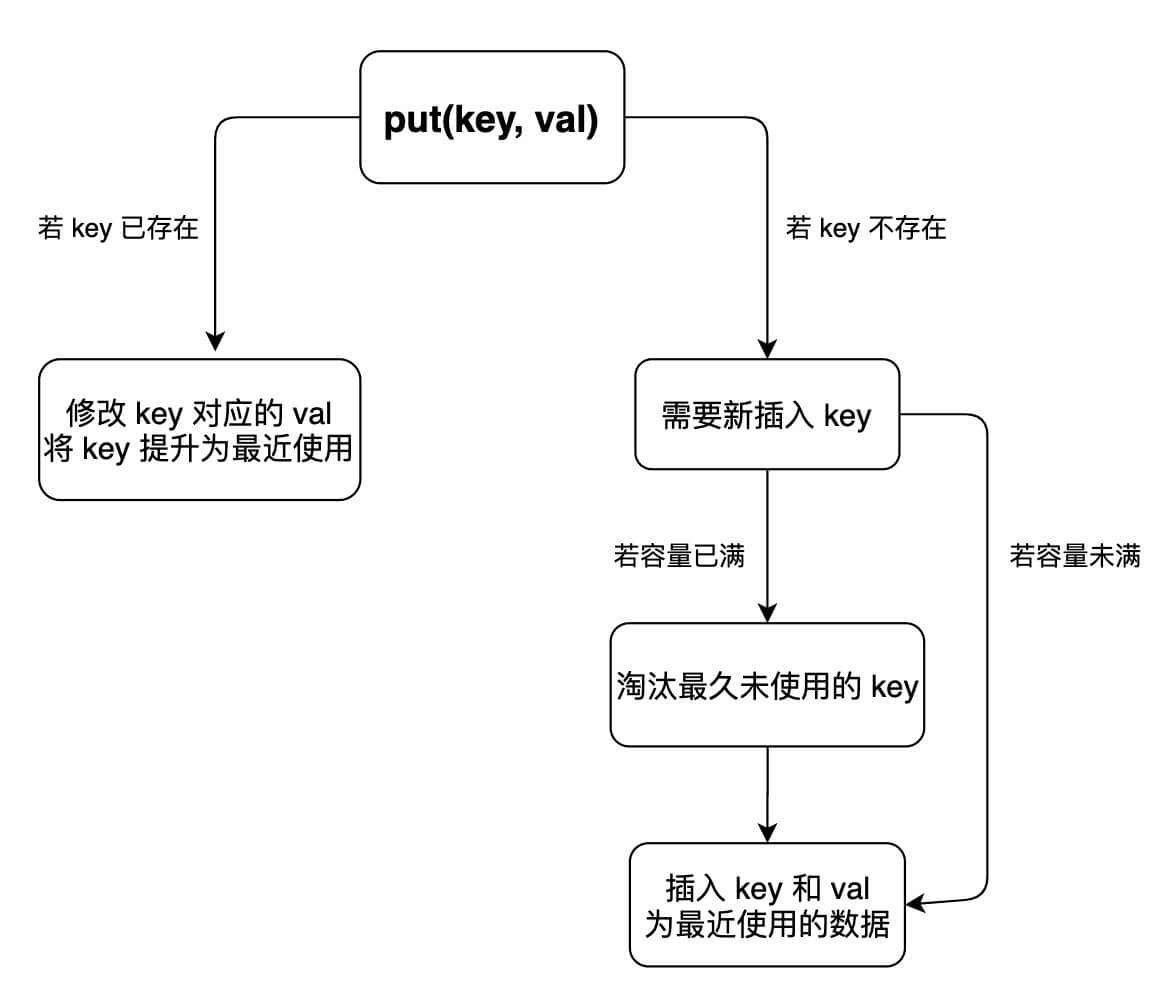
2.3、put方法逻辑

public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if(node == null){
            //创建新节点
            DLinkedNode newNode = new DLinkedNode(key,value);
            //哈希表加入结点
            cache.put(key,newNode);
            //结点addToHead
            linkedList.addToHead(newNode);
            size++;
            if(size > capacity){
                //删除尾部结点
                DLinkedNode tail = linkedList.removeTail();
                //哈希表删除结点
                cache.remove(tail.key);
                size--;
            }
        }else{
            node.val = value;
            //结点moveToHead
            linkedList.moveToHead(node);
        }
 }

2.4、完整实现

class LRUCache {

    private Map<Integer,DLinkedNode> cache;//哈希表缓存

    private DLinkedList linkedList;//双链表

    private int size;//链表size
    private int capacity;//链表容量

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        this.cache = new HashMap<>();
        this.linkedList = new DLinkedList();
    }
    
    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if(node == null) return -1;
        //节点moveToHead
        linkedList.moveToHead(node);
        return node.val;
    }
    
    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if(node == null){
            //创建新节点
            DLinkedNode newNode = new DLinkedNode(key,value);
            //哈希表加入结点
            cache.put(key,newNode);
            //结点addToHead
            linkedList.addToHead(newNode);
            size++;
            if(size > capacity){
                //删除尾部结点
                DLinkedNode tail = linkedList.removeTail();
                //哈希表删除结点
                cache.remove(tail.key);
                size--;
            }
        }else{
            node.val = value;
            //结点moveToHead
            linkedList.moveToHead(node);
        }
    }

   class DLinkedList{//双链表

       DLinkedNode head,tail;//链表首尾结点

       public DLinkedList(){
           this.head = new DLinkedNode(-1,-1);
           this.tail = new DLinkedNode(-1,-1);
           head.next = tail;
           tail.pre = head;
       }

       public void addToHead(DLinkedNode node){//将节点添加到头部
           node.pre = head;
           node.next = head.next;
           head.next.pre = node;
           head.next = node;
       }

       public void moveToHead(DLinkedNode node){//将某个访问后的节点添加到头部
           removeNode(node);
           addToHead(node);
       }

       public void removeNode(DLinkedNode node){//删除某个节点
           node.pre.next = node.next;
           node.next.pre = node.pre;
       }

       public DLinkedNode removeTail(){//删除尾部结点
           DLinkedNode res = tail.pre;
           removeNode(res);
           return res;
       }

   }

    class DLinkedNode{//双链表节点类
        int key,val;
        DLinkedNode pre,next;
        
        public DLinkedNode(int _key,int _val){
            this.key = _key;
            this.val = _val;
        }

    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */